3.3 The Linear Programming Model

Tackling a multi-knapsack problem with a LP solver amounts to implementing a branch & bound solver to obtain integral solutions. The idea is to compute a continuous solution and to branch over the problem variables with continuous solutions. This is done until only integral problem variables are left. This is what the procedure DistributeKnapSackLP does.

declare 
proc {DistributeKnapSackLP Vs ObjFn Constraints MaxProfit}
   choice 
      DupVs = {DuplicateRIs Vs}
      DupMaxProfit V DupV
   in 
      DupMaxProfit = {RI.var.bounds
                      {RI.getLowerBound MaxProfit}
                      {RI.getUpperBound MaxProfit}}
       
      {LP.solve DupVs ObjFn Constraints DupMaxProfit optimal}
 
      V#DupV = {SelectVar Vs#DupVs}
 
      case {IsDet V} then 
         DupMaxProfit = MaxProfit
         DupVs        = Vs
      else 
         choice 
            {RI.lessEq {Ceil DupV} V}  
         [] 
            {RI.lessEq V {Floor DupV}}  
         end 
         {DistributeKnapSackLP Vs ObjFn Constraints MaxProfit}
      end 
   end 
end

It first duplicates the problem variables (note this is possible due to stability) and invokes the LP solver on them to compute a (possibly continuous) solution. Then it selects the first duplicated continuous problem variable DupV by SelectVar (see below). If continuous variables are left (see the else branch of the case statement), it creates two choices on the corresponding original problem variable V: 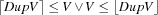$\lceil DupV \rceil \le V \vee V \le \lfloor DupV \rfloor$ and calls DistributeKnapSackLP recursively. In case no continuous variables are left, an integral solution is found and the original problem variables are unified with duplicated ones.

For completeness sake the auxiliary functions SelectVar and DuplicateRIs are presented here.

declare 
fun {SelectVar VsPair}
   case VsPair
   of nil#nil then unit#unit  
   [] (VH|VT)#(RVH|RVT) then 
      % check for integrality
      case RVH == {Round RVH}
      then {SelectVar VT#RVT}
      else VH#RVH end 
   else unit 
   end 
end

declare 
fun {DuplicateRIs Vs}
   {Map Vs
    fun {$ V}
       {RI.var.bounds
        {RI.getLowerBound V}
        {RI.getUpperBound V}}
    end}
end

The procedure KnapsackLP return the script which creates the appropriate parameters for the LP solver and eventually calls DistributeKnapSackLP.

declare 
fun {KnapsackLP Problem}
   NumProducts = {Length Problem.profit}
   Resources   = Problem.resources
in 
   proc {$ Sol}
      sol(maxprofit: MaxProfit = {RI.var.decl}
          products: Products = {MakeList NumProducts})
      = Sol
 
      ObjFn Constraints
   in 
      {ForAll Products proc {$ V}
                          {RI.var.bounds 0.0 RI.sup V}
                       end}
 
      ObjFn = objfn(row: {Map Problem.profit IntToFloat}
                    opt: max)
       
      Constraints =  
      {Map {Arity Resources}
       fun {$ ResourceName}
          Resource = Resources.ResourceName
       in 
           constr(row: {Map Resource.npp IntToFloat}
                  type: '=<' 
                  rhs: {IntToFloat Resource.ta})
       end}
       
      {DistributeKnapSackLP Products ObjFn Constraints
       MaxProfit}
   end 
end

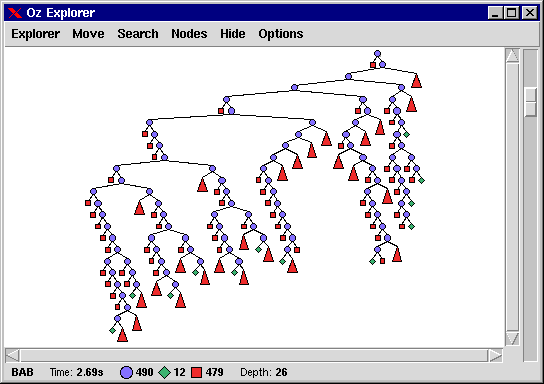
Feeding

{ExploreBest {KnapsackLP Problem} proc {$ O N} {RI.lessEq O.maxprofit+1.0 N.maxprofit} end}

produces the following search tree.