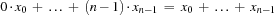The first redundant constraint follows from the fact that the total number of occurrences in the sequence is
, and that no numbers but those between 0 and
occur in the sequence.
The second redundant constraint follows from the fact that
Here is a parametrized script for the Magic Sequence Puzzle:
fun {MagicSequence N}
Cs = {List.number ~1 N-2 1}
in
proc {$ S}
{FD.tuple sequence N 0#N-1 S}
{For 0 N-1 1
proc {$ I} {FD.exactly S.(I+1) S I} end}
%% redundant constraints
{FD.sum S '=:' N}
{FD.sumC Cs S '=:' 0}
%%
{FD.distribute ff S}
end
end