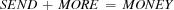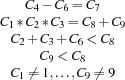1 Introduction
This document is a first introduction to constraint-based problem solving and its implementation in Oz. We restrict our attention to combinatorial problems that can be stated with variables ranging over finite sets of nonnegative integers. Problems in this class range from puzzles to real world applications as diverse as scheduling, ware house allocation, configuration and placement.
The two basic techniques of constraint programming are constraint propagation and constraint distribution. Constraint propagation is an efficient inference mechanism obtained with concurrent propagators accumulating information in a constraint store. Constraint distribution splits a problem into complementary cases once constraint propagation cannot advance further. By iterating propagation and distribution, propagation will eventually determine the solutions of a problem.
Constraint distribution can easily lead to an exponential growth of the number of subproblems to be considered. Fortunately, this potential combinatorial explosion can often be contained by combining strong propagation mechanisms with problem specific heuristics for selecting distribution steps.
The following puzzles give a first idea of the combinatorial problems we will solve in this document:
Money
The Send More Money Problem consists in finding distinct digits for the letters 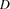 ,
,  ,
, 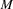 ,
, 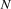 ,
, 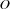 ,
,  ,
,  ,
,  such that
such that  and
and 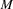 are different from zero (no leading zeros) and the equation
are different from zero (no leading zeros) and the equation
is satisfied. The unique solution of the problem is 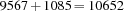 .
.
Safe
The code of Professor Smart's safe is a sequence of 9 distinct nonzero digits 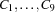 such that the following equations and inequations are satisfied:
such that the following equations and inequations are satisfied:
Can you determine the code?
Coloring
Given a map showing the West European countries Netherlands, Belgium, France, Spain, Portugal, Germany, Luxemburg, Switzerland, Austria, and Italy, find a coloring such that neighboring countries have different color and a minimal number of colors is used.
Grocery
A kid goes into a grocery store and buys four items. The cashier charges $7.11, the kid pays and is about to leave when the cashier calls the kid back, and says ``Hold on, I multiplied the four items instead of adding them; I'll try again; Hah, with adding them the price still comes to $7.11''. What were the prices of the four items?
Queens
Place 8 queens on a chess board such that no two queens attack each other.
The problems have in common that they can be stated with variables that are a priori constrained to finite sets of nonnegative integers. Consequently, the problems could be solved by simply checking all possible combinations of the values of the variables. This naive generate and test method is however infeasible for most realistic problems since there are just too many possible combinations.
More Information
While this tutorial tries to be as self-contained as possible for constraint programming in Oz, it is expected that the reader has already a working knowledge of functional Oz programming. As an introduction for functional and object-oriented programming in Oz we suggest ``Tutorial of Oz''. The full functionality of Oz provided for constraint programming is included in the document Part II of ``System Modules''.
The Examples
The tutorial features a large number of examples. To ease the understanding the examples should be tried in the Oz Programming Environment (OPI). The Oz programs are contained in the following file. Oz programs for some solutions to the exercises are contained in the following file.
Acknowledgements
The tutorial is based on the document ``Finite Domain Constraint Programming in Oz. A Tutorial'' by Gert Smolka, Christian Schulte, and Jörg Würtz for a previous version of Oz.