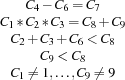3.6 Example: Safe

Problem Specification

The code of Professor Smart's safe is a sequence of 9 distinct nonzero digits 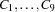$C_1,\ldots,C_9$ such that the following equations and inequations are satisfied:

$\begin{array}{rcl} & C_4 - C_6 = C_7\\ & C_1 * C_2 * C_3 = C_8 + C_9\\ & C_2 + C_3 + C_6 < C_8\\ & C_9 < C_8\\ & C_1\neq1,\ldots, C_9\neq9 \end{array}$

Can you determine the code?

Model and Distribution Strategy

We choose the obvious model that has a variable for every digit 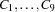$C_1,\ldots,C_9$ . We distribute over these variables with the standard first-fail strategy.

proc {Safe C}
   {FD.tuple code 9 1#9 C}
   {FD.distinct C}
   C.4 - C.6 =: C.7
   C.1 * C.2 * C.3 =: C.8 + C.9
   C.2 + C.3 + C.6 <: C.8
   C.9 <: C.8
   {For 1 9 1 proc {$ I} C.I \=: I end}
   {FD.distribute ff C}
end

Figure 3.5: A script for the Safe Puzzle.

Script

Figure 3.5 shows a script for the Safe Puzzle. The statement

{FD.tuple code 9 1#9 C}

constrains the root variable C to a tuple with label code whose components are integers in the domain 1#9. The statement

{For 1 9 1 proc {$ I} C.I \=: I end}

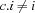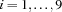posts the constraint $c.i\neq i$ for every $i=1,\ldots,9$ .

The full search tree of Safe has 23 nodes and contains the unique solution:

code(4 3 1 8 9 2 6 7 5)