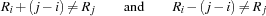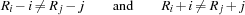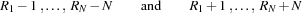5.1 Example: Queens
Problem Specification
Place 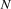 queens on an
queens on an 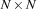 chess board such that no two queens attack each other. The parameter of the problem is
chess board such that no two queens attack each other. The parameter of the problem is 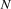 . A solution for the 8-queens problem looks as follows:
. A solution for the 8-queens problem looks as follows:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
1 |  |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|  |
|
3 |
|
|
|  |
|
|
|
|
4 |
|
|
|
|
|  |
|
|
5 |
|
|
|
|
|
|
|  |
6 |
|  |
|
|
|
|
|
|
7 |
|
|
|
|  |
|
|
|
8 |
|
|  |
|
|
|
|
|
Figure 5.1.
Model
We will use a clever model avoiding possible symmetries and minimizing the number of propagators.
We assume that the queens are numbered from 1 to 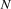 , and that the
, and that the 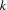 -th queen is always placed in the
-th queen is always placed in the 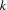 -th column. For every queen
-th column. For every queen  we have one variable
we have one variable 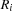 saying in which row the queen is placed. The model guarantees by construction that two queens are never placed in the same column. To ensure that two queens are never in the same row, we impose the constraint that the variables
saying in which row the queen is placed. The model guarantees by construction that two queens are never placed in the same column. To ensure that two queens are never in the same row, we impose the constraint that the variables 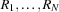 are pairwise distinct.
are pairwise distinct.
To enforce that two queens are never in the same diagonal, we need to impose the constraints
for all  ,
, 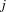 such that
such that 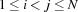 . Equivalently, we can impose the constraints
. Equivalently, we can impose the constraints
for all  ,
, 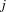 such that
such that 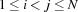 . This is equivalent to saying that the sequences
. This is equivalent to saying that the sequences
are both nonrepetitive. Since Oz has a special propagator for the constraint stating the nonrepetitiveness of such sequences, this formulation requires only two propagators, one for each sequence.
Distribution Strategy
We distribute on the variables 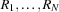 using a first-fail strategy that tries the value in the middle of the domain of the selected variable first. This strategy works well even for large N.
using a first-fail strategy that tries the value in the middle of the domain of the selected variable first. This strategy works well even for large N.
fun {Queens N}
proc {$ Row}
L1N ={MakeTuple c N}
LM1N={MakeTuple c N}
in
{FD.tuple queens N 1#N Row}
{For 1 N 1 proc {$ I}
L1N.I=I LM1N.I=~I
end}
{FD.distinct Row}
{FD.distinctOffset Row LM1N}
{FD.distinctOffset Row L1N}
{FD.distribute generic(value:mid) Row}
end
end
Figure 5.2: A script for the N-queens Problem.
Script
Figure 5.2 shows a parameterized script for the N-Queens Problem. The actual script is created by the procedure Queens, which takes N as parameter. The script constrains its root variable Row to a tuple having a component for every queen. This implicitly creates the variables 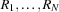 of the model.
of the model.
The statements
{FD.distinct Row}
{FD.distinctOffset Row LM1N}
{FD.distinctOffset Row L1N}create propagators for the constraints stating that the sequences
| ... |
|
| ... |
|
| ... |
|
be non repetitive.