6.1 Example: Coloring a Map

Problem Specification

Given a map showing the West European countries Netherlands, Belgium, France, Spain, Portugal, Germany, Luxemburg, Switzerland, Austria, and Italy, find a coloring such that neighboring countries have different color and a minimal number of colors is used.

Model

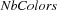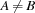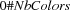We have a variable NbColors saying how many different colors we can use. Moreover, we have a variable for every country. For every pair , of countries having a border in common we impose the constraint $A\neq B$ . We represent colors as numbers. Hence we constrain all variables for countries to integers in $0\#{NbColors}$ .

Distribution Strategy

We first distribute on 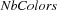NbColors , trying the numbers 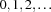$0,1,2,\ldots$ in ascending order. After 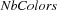is determined, we distribute on the variables for the countries using the usual first-fail strategy.

fun {MapColoring Data}
   Countries = {Map Data fun {$ C#_} C end}
in 
   proc {$ Color}
      NbColors  = {FD.decl}
   in 
      {FD.distribute naive [NbColors]}
      %% Color: Countries --> 1#NbColors
      {FD.record color Countries 1#NbColors Color}
      {ForAll Data
       proc {$ A#Bs}
          {ForAll Bs proc {$ B} Color.A \=: Color.B end}
       end}
      {FD.distribute ff Color}
   end 
end 
 
Data = [ austria     # [italy switzerland germany]
         belgium     # [france netherlands germany luxemburg]
         france      # [spain luxemburg italy]
         germany     # [austria france luxemburg netherlands]
         italy       # nil
         luxemburg   # nil
         netherlands # nil
         portugal    # nil
         spain       # [portugal]
         switzerland # [italy france germany austria] ]

Figure 6.1: A script for the Map Coloring Problem together with a data specification.

Script

The script appears in Figure 6.1. It is parameterized with the specification of the map to be colored. The figure shows the specification of a map containing some European countries.

The script first creates a local variable NbColors that specifies the number of different colors to be used for coloring the map. Then it distributes naively on NbColors. Recall that a distributor blocks its thread until it has done its job. After NbColors is determined by distribution, the variable Color is constrained to a record mapping the country names to integers in 1#NbColors. This implicitly creates the variables for the Countries. Next the script creates a propagator

Color.A \=: Color.B

for every pair A, B of bordering countries. Finally, the script distributes on Color using the first-fail strategy.

The statement

{ExploreOne {MapColoring Data}}

will show the search tree explored to find the first solution, which looks as follows:

color( austria: 1 belgium: 3 france: 1 germany: 2 italy: 2 luxemburg: 4 netherlands: 1 portugal: 1 spain: 2 switzerland: 3 )

The search tree of MapColoring is interesting. First, colorings with 0, 1, 2 and 3 colors are searched and not found. Then a coloring with 4 colors is searched. Now a solution is found quickly, without going through further failure nodes. There are many solutions using 4 colors since the particular color given to a country does not matter.