A Traps and Pitfalls
This section lists traps and pitfalls that beginners typically fall into when writing their first finite domain problem scripts in Oz.
Ordinary Arithmetic Blocks
There is a big difference between the statement
X+Y =: Zand the statement
X+Y = Z The first statement creates a concurrent finite domain propagator and never blocks. The second statement creates an addition task that blocks until its arguments X and Y are known. Blocking means that the statements following the addition statement will not be executed.
This pitfall can be particulary malicious if the infix expressions (X mod Y) or (X div Y) are used. For instance,
X mod Y =: Zis equivalent to
local A in
X mod Y = A
A =: Z
end and will thus block until X and Y are determined. In contrast, a statement like
U + X*(Y-Z) =: ~Y is fine since the operations +, *, -, and ~ are implemented by the created propagator. The general rule behind this is simple: The infix operators =:, \=:
:, >:, =<:, and >=: absorp the arithmetic operators +, -, *, and ~, and no others.
Incidentally, interval and domain propagators for the modulo constraint can be created with the procedures {FD.modI X Y Z} and {FD.modD X Y Z}, respectively (see Section 2.4).
There is an easy way to check whether a statement in a script blocks: Just insert as last statement
{Browse 'End of script reached'} and check in the Browser. If 'End of script reached' appears in the Browser when you execute the script (e.g. with the Explorer), no statement in the script can have blocked, except for those that have been explicitly parallelized with thread ... end.
Delay of Propagators
Almost all propagators start their work only after all variables occurring in the implemented constraint are constrained to finite domains in the constraint store. For instance, the propagator created by
X*47 =: _ will never start propagation since it will wait forever that the anonymous variable created by the wildcard symbol _ is constrained to a finite domain. This problem can easily be avoided by writing
X*47 =: {FD.decl} The procedure {FD.decl X} constrains its argument to the largest finite domain possible (i. e. 0#sup).
The Operators =: and :: don't Introduce Pattern Variables
The statement
local X =: Y+Z in...end
does not declare X as local variable, which is in contrast to the statement
local X = Y+Z in...end
which however does not create a propagator. The desired effect can be obtained by writing
local X = {FD.decl} in X =: Y+Z...end
A related pitfall is the wrong assumtion that a statement
local X :: 4#5 in...end
declares X as local variable. This is not the case. To obtain the desired effect, you can write
local X = {FD.int 4#5} in...end
Delay of Domain Specifications
A domain specification like X::L#U constrains X only after both L and U are determined. Thus
L :: 5#13
U :: 14#33
X :: L#U will constrain X only after both L and U have been determined.
Coreferences are not Always Realized
The propagator created by
A*A + B*B =: C*Cprovides much less propagation than the four propagators created by
{FD.times A A} + {FD.times B B} =: {FD.times C C} The reason is that the first propagator does not realize the coreferences in the constraint it implements, that is, it treats the two occurrences of A, say, as if they were independent variables. On the other hand, the propagator created by {FD.times A A $} exploits this coreference to provide better propagation. The Pythagoras Puzzle (see Section 7.2) is a problem, where exploiting coreferences is essential).
Large Numbers
There is an implementation-dependent upper bound for the integers that can occur in a finite domain stored in the constraint store. This upper bound is available as the value of FD.sup. In Mozart, FD.sup is 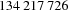 on Linux and Sparc platforms.
on Linux and Sparc platforms.
The same restriction applies to constants appearing in propagators. For instance, the creation of a propagator
X*Y <: 900*1000*1000 will result in a run-time error since the constant 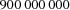 computed by the compiler is larger than
computed by the compiler is larger than FD.sup. There is a trick that solves the problem for some cases. The trick consists in giving a large number as a product involving an auxiliary variable:
local A = 900 in
X*Y <: A*1000*1000
end The trick exploits that propagators can compute internally with integers larger than FD.sup, and that the compiler does not eliminate the auxiliary variable. The Grocery Puzzle in Section 4.1 uses this trick.