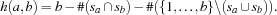3 Generating Hamming Codes

Problem Specification

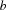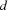Generate a Hamming code that fits in -bit words to code symbols where the Hamming distance between every two symbol codes is at least . The Hamming distance between to words is the number of bit positions where they differ.

Model

A 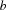-bit word is modeled by a set 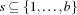where 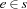means that the bit at position is set (resp. unset otherwise). The Hamming distance 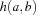between two words and 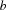represented as sets 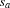and 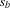can be computed by subtracting from the word size 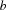the number of elements that is contained (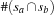) resp. is not contained (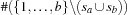) in both sets. Thus, the Hamming distance results in

Solver

The function Hamming returns a solver to generate a Hamming code for NumSymbols symbols in words with Bits bits and a Hamming distance of Distance. The procedure MinDist implements the constraint that the Hamming distance does not exceed the value of Distance. The list Xs holds the sets representing the single codes. The nested loop (ForAllTail and ForAll) imposes MinDist on all pairwise distinct elements of Xs. The distribution employs straightforwardly a naive strategy.

declare 
fun {Hamming Bits Distance NumSymbols}       
   proc {MinDist X Y}       
      Common1s = {FS.intersect X Y}
      Common0s = {FS.complIn
                  {FS.union X Y}
                  {FS.value.make [1#Bits]}}
   in 
      Bits-{FS.card Common1s}-{FS.card Common0s}>=:Distance
   end 
in 
   proc {$ Xs}
      Xs = {FS.var.list.upperBound NumSymbols [1#Bits]}
       
      {ForAllTail Xs proc {$ X|Y}
                        {ForAll Y proc {$ Z}
                                     {MinDist X Z}
                                  end}
                     end}
       
      {FS.distribute naive Xs}
   end 
end 

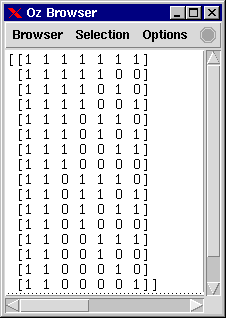
The following code generates a Hamming code for 16 symbols using 7 bit words and ensures a Hamming distance of 2.

{Browse
 {Map {SearchOne {Hamming 7 2 16}}.1
  fun {$ X}  
     {ForThread 7 1 ~1 fun {$ Is I}  
                          {FS.reified.isIn I X}|Is  
                       end nil}  
  end}}

Further, the code is nicely formatted displayed in the Oz Browser.