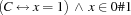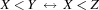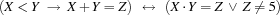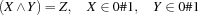8.1 Getting Started

reification of a constraint

The reification of a constraint with respect to a variable is the constraint

$(C \leftrightarrow x=1) \;\land\;x\in0\#1$

where it is assumed that does not occur free in .

The operational semantics of a propagator for the reification of a constraint with respect to is given by the following rules:

If the constraint store entails 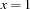, the propagator for the reification reduces to a propagator for .
If the constraint store entails 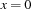, the propagator for the reification reduces to a propagator for $\neg C$ }.
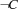If a propagator for would realize that the constraint store entails , the propagator for the reification tells 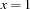and ceases to exist.
If a propagator for would realize that the constraint store is inconsistent with , the propagator for the reification tells 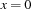and ceases to exist.

To understand these rules, you need to be familiar with the definitions in Section 2.2.

0/1-variables

A 0/1-variable is a variable that is constrained to the finite domain 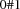$0\#1$ . The control variables of reified constraints are 0/1-variables.

posting refied constraints

Here are examples for statements creating propagators for reified constraints:

(X<:Y)=B creates a propagator for the reification of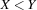 with respect to .
(X+Y+Z=:0)=B creates a propagator for the reification of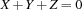 with respect to .
(X\=:Y)=B creates a propagator for the reification of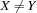 $X\neq Y$ with respect to .
(X::0#10)=B creates a propagator for the reification of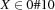 $X\in0\#10$ with respect to .
{FD.reified.distance X Y '=:' Z B} creates a propagator for the reification of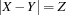 with respect to .

expressing equivalences

With reified constraints it is straightforward to express equivalences of constraints. For instance, the equivalence

$X<Y\;\leftrightarrow\; X<Z$

can be posted with the statement

X<:Y = X<:Z

This statement is a notational convenience for

local B in X<:Y=B X<:Z=B end

and creates 2 propagators for reified constraints.

Boolean connectives

We can define the Boolean connectives (e.g., conjunction or negation) by associating 0 with false and 1 with true. The respective Boolean constraints can be posted by means of the following procedures:

{FD.conj X Y Z} posts the constraint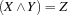 $(X\land Y)=Z$ .
{FD.disj X Y Z} posts the constraint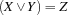 $(X\lor Y)=Z$ .
{FD.impl X Y Z} posts the constraint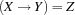 $(X\to Y)=Z$ .
{FD.equi X Y Z} posts the constraint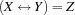 $(X\leftrightarrow Y)=Z$ .
{FD.nega X Y} posts the constraint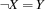 $\neg X=Y$ .

Exercises

Exercise 8.1 (See solution)

Write a statement that posts the constraint
$(X<Y\;\to\; X+Y=Z) \;\;\leftrightarrow\;\; (X\cdot Y=Z\;\lor\;Z\neq 5)$

Exercise 8.2 (See solution)

Write a procedure {Conj X Y Z} that posts the constraints
$(X\land Y)=Z ,\quad X\in0\#1 ,\quad Y\in0\#1$
The procedure should post the conjunction $(X\land Y)=Z$ . by means of the reified form of the infix operator =:.
Write analogous procedures Equi and Nega posting equivalences and negations.
Write an analogous procedure Dis posting a disjunction $(X\lor Y)=Z$ . Use the reified form of <: to post the disjunction.
How would you write a procedure posting an implication $(X\to Y)=Z$ ?